Na resolução de uma equação do 2º grau temos três possibilidades de resultados, podemos encontrar duas raízes reais diferentes, duas raízes reais iguais ou nenhuma raiz real.
Quando existir raiz real na resolução de equações do 2º grau, podemos fazer relações entre essas raízes, como: soma (x’ + x”) e produto (x’ . x”).
Para provarmos a soma e o produto de duas raízes reais de uma equação do 2º grau devemos partir da sua forma geral:
ax2 + bx + c = 0
Dessa forma geral, podemos encontrar duas raízes reais x’ e x”, utilizando Bháskara.
SOMA
Somando as duas raízes:
x’ + x”
- b - √∆ - b + √∆ → +√∆ e -√∆ cancelam, pois sua soma será zero.
2a
-2b :2
2a :2
-b
a
Portanto, somar as duas raízes de uma equação do segundo grau é o mesmo que:
x’ + x” = -b
a
PRODUTO
Multiplicando as duas raízes:
x’ . x”
Portanto, o produto das duas raízes de uma equação do segundo grau é o mesmo que:
x’ . x” = c
a
Além de utilizarmos a fórmula de Bháskara para encontrarmos o valor de x’ e x”, podemos utilizar o produto e a soma das raízes, veja como:
Dada a equação x2 – 7x + 10 = 0. Para encontrar a soma e o produto de suas raízes não é necessário que saibamos qual é o valor delas, mas devemos retirar da equação os seus coeficientes.
a = 1
b = - 7
c = 10
Chegamos a duas conclusões: a soma dessas raízes será 7 e o produto delas será 10. Por tentativas podemos encontrar números que multiplicados resultem em 10.
5 . 2 = 10
(-5) . (-2) = 10
1 . 10 = 10
(-1) . (-10) = 10
Desses produtos deve-se escolher aquele que se somarmos os seus fatores encontraremos como resultado 7.
5 + 2 = 7
Portanto, x’ = 5 e x” = 2.

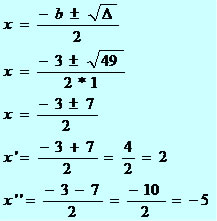
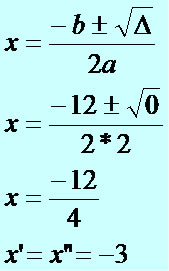






.jpg)
.png)

